データ分析入門２：分布を確認する

前回、「集計したデータを言い表す代表的な値には平均値、中央値、最頻値があるが、ひとつの値だけを確認しても不十分であり、ヒストグラムを作って分布状態を確かめる必要がある」ということを説明しました。

仮に、2つのグループを集計し、平均値も中央値も同じだったとしても、分布が全く異なっていることがあるからです。

では、その分布を無視すると、どんな困ったことがあるのか。それをご説明しましょう。

今から10年前。ある企業の製品がA国の中間層(年間世帯収入400～700万円)に支持されて市場参入に成功していたとします。新たにB国の市場に参入しようと考え、B国の国民の年間の世帯収入を調査したところ、B国の世帯収入の平均値も中央値も、すでに市場参入に成功しているA国の値と同じでした。そこで、「A国で当社の製品を買ってくれている顧客と同様の客層に対して、同様のチャネル、同様の価格、同様のプロモーションで参入できるだろう」と考えました。

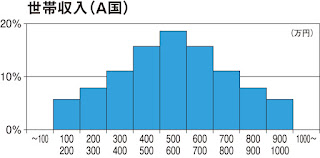
しかし実は、B国の収入階級ごとの人口分布は図のように、A国とはまったく異なるものでした。このことを知らずにB国に参入した結果、どんなことが起こったでしょうか?

分布を見てお分かりのように、A国では中間層は大きなボリュームですが、B国には中間層が非常に少なくとても小さな市場です(貧富の差が激しい国ではこのような分布になります)。B国に投入した商品は、低所得層には高すぎて手が出ないもので、富裕層には安っぽいものに映る可能性があります。

ヒストグラムが、峰が1つの山型(単峰性)でない場合、この集計の中には異質なグループがあると推測できます。先のB国の例でいえば、高収入層と低収入層です。パチンコ・パチスロユーザーの「1カ月の遊技予算」（負け許容額）を調べても、きれいな単峰性の山型にはなりません(図) 。回答者の中には、4円貸ユーザーと低玉貸ユーザーという、消費金額の面で異質なグループが混在しているからです。

実際に、大手パチンコポータルサイト上でパチンコ・パチスロユーザーの遊技実態調査を実施したところ、1カ月の遊技予算の全体平均は4万3034円でした（2014年に実施） 。パチンコのみを遊技するユーザーの中で、4円貸のMAXタイプをメインで遊ぶユーザーと低貸をメインで遊ぶユーザーの1カ月の遊技予算を調べると、平均額はそれぞれ5万6932

円、2万7676円と大きな開きがありました。

(担当＝田中剛・アミューズメントジャパン編集部)

データ分析入門１：平均値、中央値、最頻値

ある集団を対象にして、あること（数値）を調べたとき、対象個々の結果を読み込んでいくのは大変です。

「つまり、どうだったんだ？」と整理するためには、要約したり視覚化する必要があります。

例えば、世帯の年間収入を調べた場合、ぴったり同じ収入額の人は少ないでしょう。「500万円の人が1人、502万円の人が1人、503万円の人が1人…」といった具合に、100人に調査すれば、100通りに近い数値が得られるはず。しかしこれでは、把握が難しいので、「500万円以上600万円未満」といった具合に、ある幅で区切って、その幅の中に該当する人は何人だったかを集計します。

こうして集計表ができますが、どの金額帯に多くの人が該当しているのかを直観的につかむには、グラフ化するのが有効で、「ヒストグラム」や「頻度分布図」と 呼ばれる縦棒グラフの一種を作ります。名前の通り、分布を把握することができます（図は1万世帯を集計して作ったヒストグラムです）。

ヒストグラムにすることで様々なことがわかります。年間収入1500万円以上の人は少数である、300万円以上～400万円未満の世帯が最も多い、次に多いのは400万円以上～500万円未満。もう少し広く捉えると、300万円以上～600万円未満あたりの世帯が多い（全体の33％くらい）、等々。

では、一般的な世帯の年間収入はどれくらいだといえるか？ 100万未満や1500万円以上の世帯もありますが、それらは全体の中では少数で、「一般的」とはいいにくい。

集計したデータを一つの数字で表現するにはいくつかの方法がありますが、３つある代表的な値の第一が「平均値」（算術平均）です。調査した個々の世帯の年間収入をすべて足し上げて、世帯数で割った値です。すると、平均値は657・6万円になります。先ほど、ヒストグラムから「300万円以上～600万 円未満あたりの世帯が多い 」ということを直観的に見てとりましたが、平均値はそれよりも多い金額です。つまり、平均値は必ずしも大多数の数値となるわけではないのです。この例で は、平均値が高めになった原因は、高収入世帯の年間収入の高さによって平均値がひっぱられてしまったためです。

第二が「中央値」です。調査した世帯の年間収入を多い順に並べて、上から数えても下から数えても真ん中の順位にいる世帯の年間収入が中央値になります。この例の場合、中央値は568万円になります。中央値は、極端な値の影響を受けません。極端な例ですが、年間収入10億円の世帯が1世帯追加されると、平均値は高くなりますが、中央値はほぼ変わりません。この例のように極端に大きな値を含んでいるデータの、時系列の変化を見る場合には、平均値よりも中央値に着目するほうが適していると言えます。

第三が「最頻値」です。年間収入がいくらの世帯が最も多いのかを見ると、300万円以上～400万円未満の世帯で、これが最頻値です。ボリュームゾーンと呼ぶこともあります。この最頻値は、集計する際に数値の幅（標準級間隔）をいくらに設定するかによって変わってくるという点に注意が必要です。

平均値、中央値、最頻値のどれを使えばよいかはケースバイケースで、どれか一つでは不十分です。左右対称の山型のヒストグラムになる場合は、平均値、中央値、最頻値はどれも近い値になります。しかし、例のようにヒストグラムの山頂が左に寄っている（右に裾が長い） 場合や逆に右に寄っている（左に裾が長い） 場合には、平均値、中央値、最頻値はズレます。ピークがふたつある二山型のヒストグラムでは、平均値と中央値は近くなりますが、最頻値はズレます。

データを集計したら平均値を求めるだけでなく、どのような分布になっているかヒストグラムで確認することを習慣にする必要があります。